Plotly – Distplots 密度图和误差条图
Plotly – Distplots 密度图和误差条图
在本章中,我们将详细了解 distplots、密度图和误差条图。让我们从学习 distplots 开始。
分布图
distplot 图工厂显示数值数据的统计表示的组合,例如直方图、核密度估计或正态曲线和地毯图。
distplot 可以由以下 3 个组件的全部或任意组合组成 –
- 直方图
- 曲线:(a)核密度估计或(b)正态曲线,以及
- 地毯图
所述figure_factory模块具有create_distplot()函数,其需要称为hist_data强制参数。
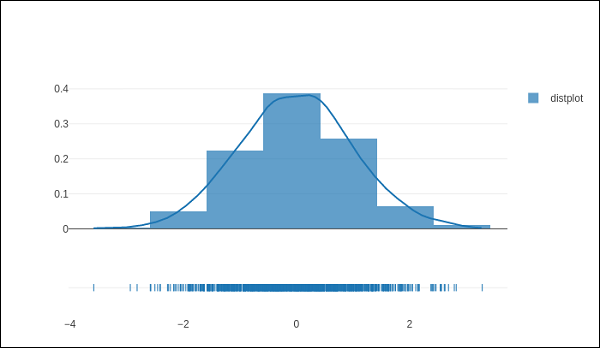
以下代码创建了一个基本的 distplot,由直方图、kde 图和 rug 图组成。
x = np.random.randn(1000) hist_data = [x] group_labels = ['distplot'] fig = ff.create_distplot(hist_data, group_labels) iplot(fig)
上述代码的输出如下 –
密度图
密度图是根据数据估计的直方图的平滑连续版本。最常见的估计形式称为核密度估计 (KDE)。在这种方法中,在每个单独的数据点绘制一条连续曲线(内核),然后将所有这些曲线加在一起以进行单个平滑的密度估计。
模块plotly.figure_factory._2d_density 中的create_2d_density()函数返回一个用于 2D 密度图的图形对象。
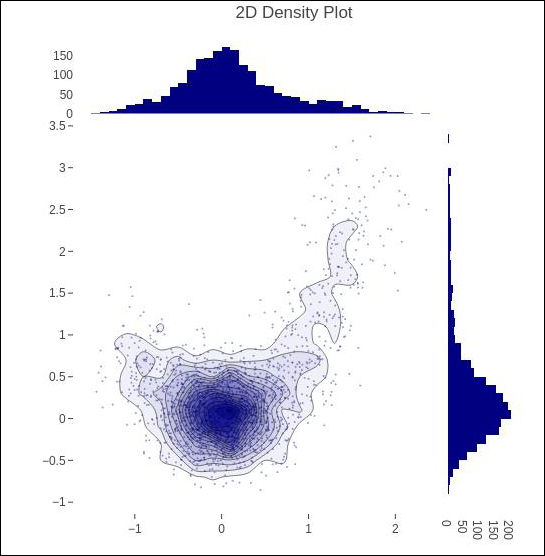
以下代码用于在直方图数据上生成二维密度图。
t = np.linspace(-1, 1.2, 2000) x = (t**3) + (0.3 * np.random.randn(2000)) y = (t**6) + (0.3 * np.random.randn(2000)) fig = ff.create_2d_density( x, y) iplot(fig)
下面提到的是上面给出的代码的输出。
误差条图
误差条是数据中误差或不确定性的图形表示,它们有助于正确解释。出于科学目的,错误报告对于理解给定数据至关重要。
误差线对问题解决者很有用,因为误差线显示了一组测量值或计算值的置信度或精度。
大多数误差线代表数据集的范围和标准偏差。它们可以帮助可视化数据如何围绕平均值分布。可以在各种图上生成误差线,例如条形图、折线图、散点图等。
所述go.Scatter()函数具有error_x和error_y性质控制如何误差棒被生成。
-
可见(布尔值) – 确定这组误差线是否可见。
类型属性有可能的值“百分比”| “常数” | ” sqrt ” | “ data ”。它设置用于生成误差线的规则。如果是“百分比”,则柱线长度对应于基础数据的百分比。在 `value` 中设置此百分比。如果是“sqrt”,则柱线长度对应于基础数据的平方。如果是“data”,条形长度用数据集`array`设置。
-
对称属性可以为真或为假。因此,误差线在两个方向上的长度或不相同(垂直条的顶部/底部,水平条的左/右。
-
数组– 设置与每个误差条长度相对应的数据。值是相对于基础数据绘制的。
-
arrayminus – 设置与垂直(水平)条的底部(左)方向上每个误差条的长度相对应的数据相对于基础数据绘制的值。
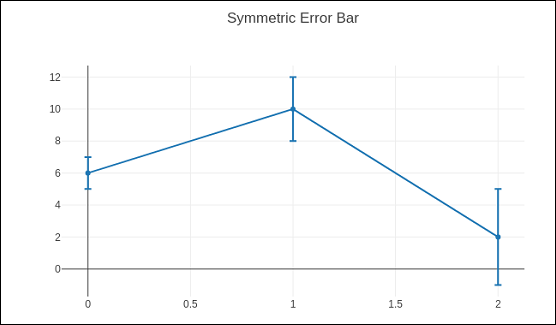
以下代码在散点图上显示对称误差条 –
trace = go.Scatter( x = [0, 1, 2], y = [6, 10, 2], error_y = dict( type = 'data', # value of error bar given in data coordinates array = [1, 2, 3], visible = True) ) data = [trace] layout = go.Layout(title = 'Symmetric Error Bar') fig = go.Figure(data = data, layout = layout) iplot(fig)
下面给出的是上述代码的输出。
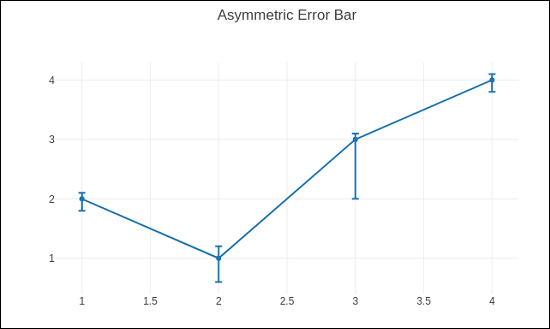
通过以下脚本呈现非对称误差图 –
trace = go.Scatter(
x = [1, 2, 3, 4],
y =[ 2, 1, 3, 4],
error_y = dict(
type = 'data',
symmetric = False,
array = [0.1, 0.2, 0.1, 0.1],
arrayminus = [0.2, 0.4, 1, 0.2]
)
)
data = [trace]
layout = go.Layout(title = 'Asymmetric Error Bar')
fig = go.Figure(data = data, layout = layout)
iplot(fig)
相同的输出如下所示 –