分析软件测量数据

在收集到相关数据后，我们必须以适当的方式对其进行分析。选择分析技术时需要考虑三个主要项目。

数据的本质

为了分析数据，我们还必须查看数据所代表的更大的人口以及该数据的分布。

抽样是从大量人口中选择一组数据的过程。样本统计数据描述和总结了从一组实验对象中获得的度量。

人口参数表示如果测量所有可能的受试者将获得的值。

总体或样本可以通过集中趋势的度量（例如均值、中位数和众数）和离散的度量（例如方差和标准差）来描述。许多数据集呈正态分布，如下图所示。

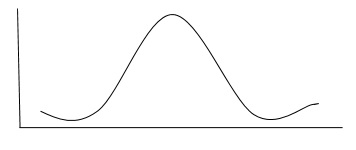
如上所示，数据将围绕均值均匀分布。这是正态分布的显着特征。

其他分布也存在数据倾斜的情况，因此平均值一侧的数据点多于另一侧。例如：如果大部分数据出现在均值的左侧，那么我们可以说分布向左偏斜。

通常，进行实验 –

为了实现其中的每一个，目标应该以假设的形式正式表达，并且分析必须直接针对假设。

调查必须旨在探索理论的真实性。该理论通常指出，某种方法、工具或技术的使用对受试者有特定的影响，使其在某些方面比其他方面更好。

有两种数据需要考虑：正常数据和非正常数据。

如果数据来自正态分布，并且有两组要比较，则可以使用学生 t 检验进行分析。如果要比较的组多于两个，则可以使用称为 F 统计量的一般方差分析检验。

如果数据是非正态的，则可以使用 Kruskal-Wallis 检验通过对数据进行排序来分析数据。

调查旨在确定描述一个或多个变量的数据点之间的关系。

可以使用三种技术来回答有关关系的问题：箱线图、散点图和相关性分析。

甲箱线图可以表示一组数据的该范围的摘要。
一个散点图表示两个变量之间的关系。
相关分析使用统计方法来确认两个属性之间是否存在真正的关系。
- 对于正态分布的值，使用Pearson 相关系数检查两个变量是否高度相关。
- 对于非正态数据，对数据进行排序并使用Spearman Rank Correlation Coefficient作为关联度量。非正态数据的另一个度量是Kendall 稳健相关系数，它调查数据点对之间的关系并可以识别偏相关。

如果排名包含大量并列值，则可以使用列联表上的卡方检验来检验变量之间的关联。类似地，线性回归可用于生成方程来描述变量之间的关系。

对于两个以上的变量，可以使用多元回归。

在选择分析技术时必须考虑调查的设计。同时，分析的复杂性会影响选择的设计。多个组使用 F 统计量，而不是对两个组使用 Student 的 T 检验。

对于具有两个以上因子的复杂因子设计，需要更复杂的关联和显着性检验。

统计技术可用于解释一组变量对其他变量的影响，或补偿时间或学习效果。