大数据分析 – K-Means 聚类

k-means 聚类旨在将 n 个观测值划分为 k 个聚类，其中每个观测值属于具有最近均值的聚类，作为聚类的原型。这导致将数据空间划分为 Voronoi 单元。

给定一组观测值(x₁， X₂， …， X_n)，其中每个观测值是一个 d 维实向量，k 均值聚类旨在将 n 个观测值划分为 k 个组G = {G₁， G₂， …， G_k}，以便最小化定义如下平方（WCSS）的内簇总和-

$$argmin \: \sum_{i = 1}^{k} \sum_{x \in S_{i}}\parallel x – \mu_{i}\parallel ^2$$

后面的公式显示了最小化的目标函数，以便在 k-means 聚类中找到最佳原型。公式的直觉是我们希望找到彼此不同的组，并且每个组的每个成员都应该与每个集群的其他成员相似。

以下示例演示了如何在 R 中运行 k-means 聚类算法。

library(ggplot2)
# Prepare Data 
data = mtcars  

# We need to scale the data to have zero mean and unit variance 
data <- scale(data)  

# Determine number of clusters 
wss <- (nrow(data)-1)*sum(apply(data,2,var)) 
for (i in 2:dim(data)[2]) { 
   wss[i] <- sum(kmeans(data, centers = i)$withinss) 
}  

# Plot the clusters 
plot(1:dim(data)[2], wss, type = "b", xlab = "Number of Clusters", 
   ylab = "Within groups sum of squares")

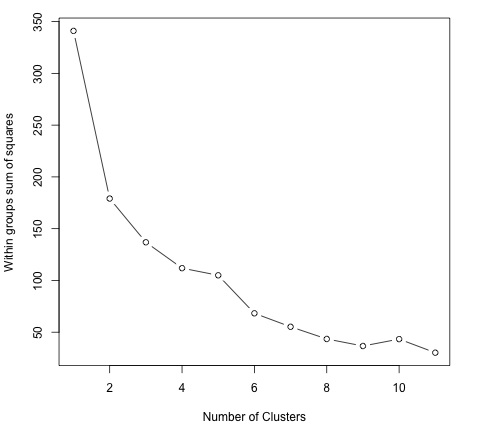
为了找到合适的 K 值，我们可以绘制不同 K 值的组内平方和。该度量通常随着添加更多组而减少，我们想找到一个点，其中组内减少的总和平方开始缓慢减少。在图中，这个值最好用 K = 6 来表示。

现在已经定义了 K 的值，需要使用该值运行算法。

# K-Means Cluster Analysis
fit <- kmeans(data, 5) # 5 cluster solution 

# get cluster means  
aggregate(data,by = list(fit$cluster),FUN = mean) 

# append cluster assignment 
data <- data.frame(data, fit$cluster)