距离向量路由(DVR)协议要求路由器通知其邻居的拓扑周期性地变化。历史上称为旧的ARPANET路由算法(或称为Bellman-Ford算法)。
Bellman Ford基础知识–每个路由器维护一个距离矢量表,该表包含其自身与所有可能的目标节点之间的距离。基于所选度量的距离是使用来自邻居距离矢量的信息来计算的。
DV路由器保存的信息- 每个路由器都有一个ID与连接到路由器的每个链接相关联, 有链接成本(静态或动态)。中级啤酒花 距离矢量表初始化-距自身= 0与所有其他路由器的距离=无限数。
距离矢量算法–
- 路由器在路由数据包中将其距离矢量传输到其每个邻居。
- 每个路由器从其每个邻居接收并保存最近接收到的距离矢量。
- 在以下情况下,路由器将重新计算其距离向量:
- 它从邻居接收距离信息,该距离向量包含与以前不同的信息。
- 它发现到邻居的链接已断开。
DV计算基于最小化每个目的地的成本
Dx(y)=估计从x到y的最小成本 C(x,v)=节点x知道每个邻居v的成本 Dx = [Dx(y):y∈N] =节点x保持距离矢量 节点x还维护其邻居的距离矢量 –对于每个邻居v,x维持Dv = [Dv(y):y∈N]
注意 –
- 有时,每个节点都会将自己的距离矢量估计值发送给邻居。
- 当节点x从任何邻居v接收到新的DV估计时,它保存v的距离矢量,并使用BF公式更新其自己的DV:每个节点y∈N的Dx(y)= min {C(x,v)+ Dv(y),Dx(y)}
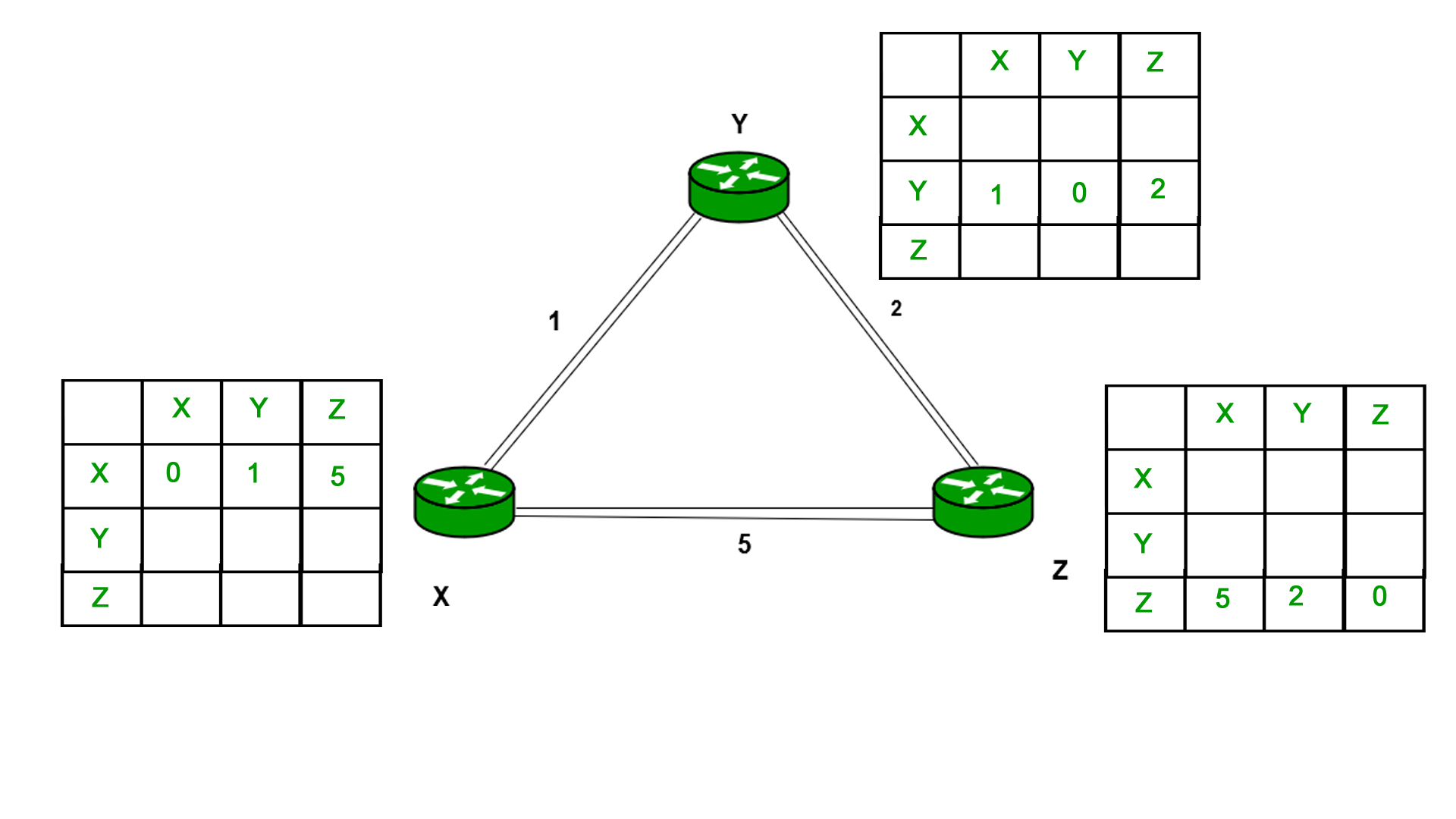
示例–如图所示,考虑3个路由器X,Y和Z。每个路由器都有其路由表。每个路由表都将包含到目标节点的距离。
考虑路由器X,X将把它的路由表共享给邻居,邻居将把它的路由表共享给邻居X,并使用Bellmenford公式计算出节点X到目的地的距离。
每个节点y∈N的Dx(y)= min {C(x,v)+ Dv(y)}
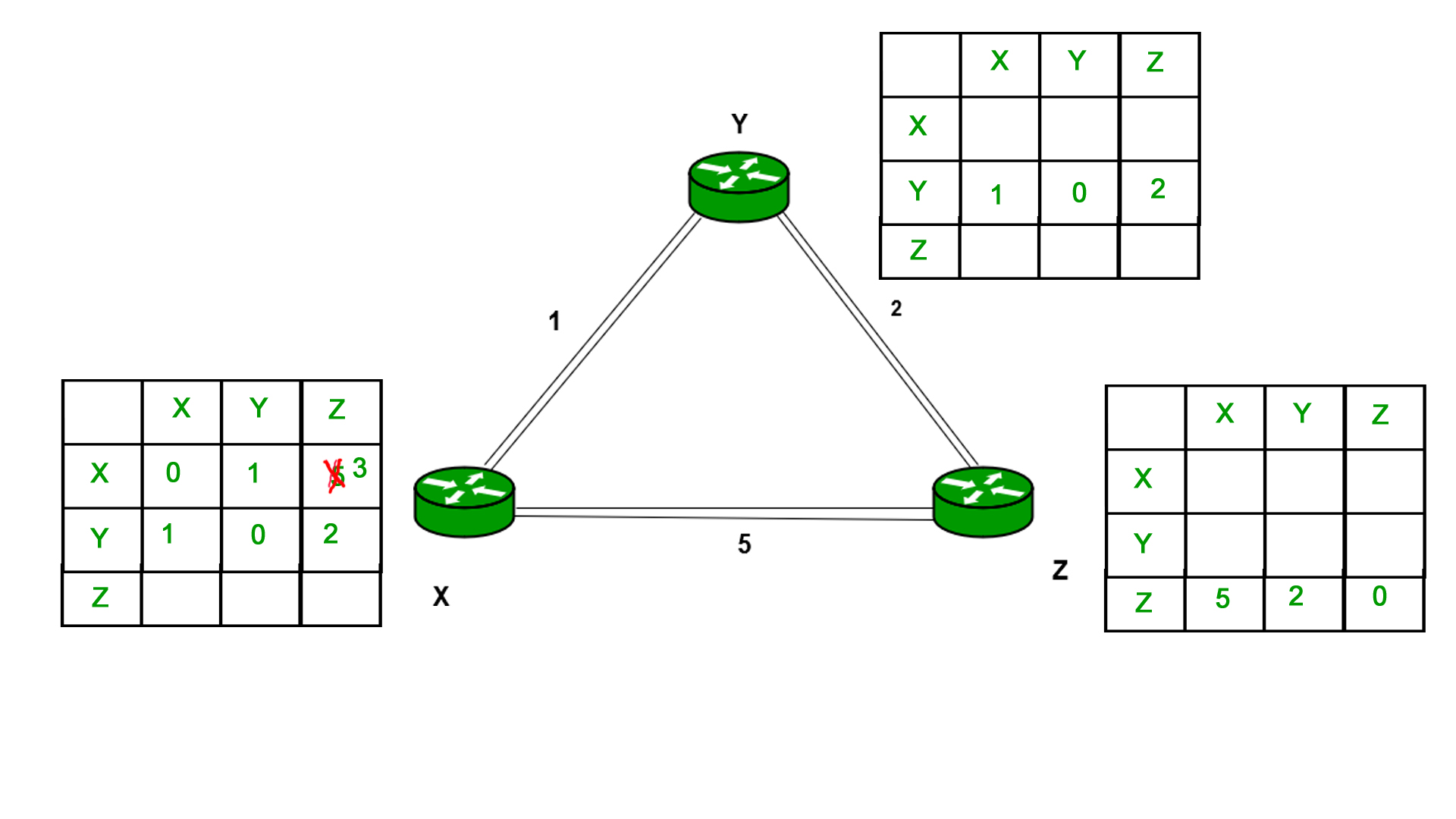
正如我们所看到的,当Y是中间节点(跳)时,从X到Z的距离将减少,因此它将在路由表X中更新。
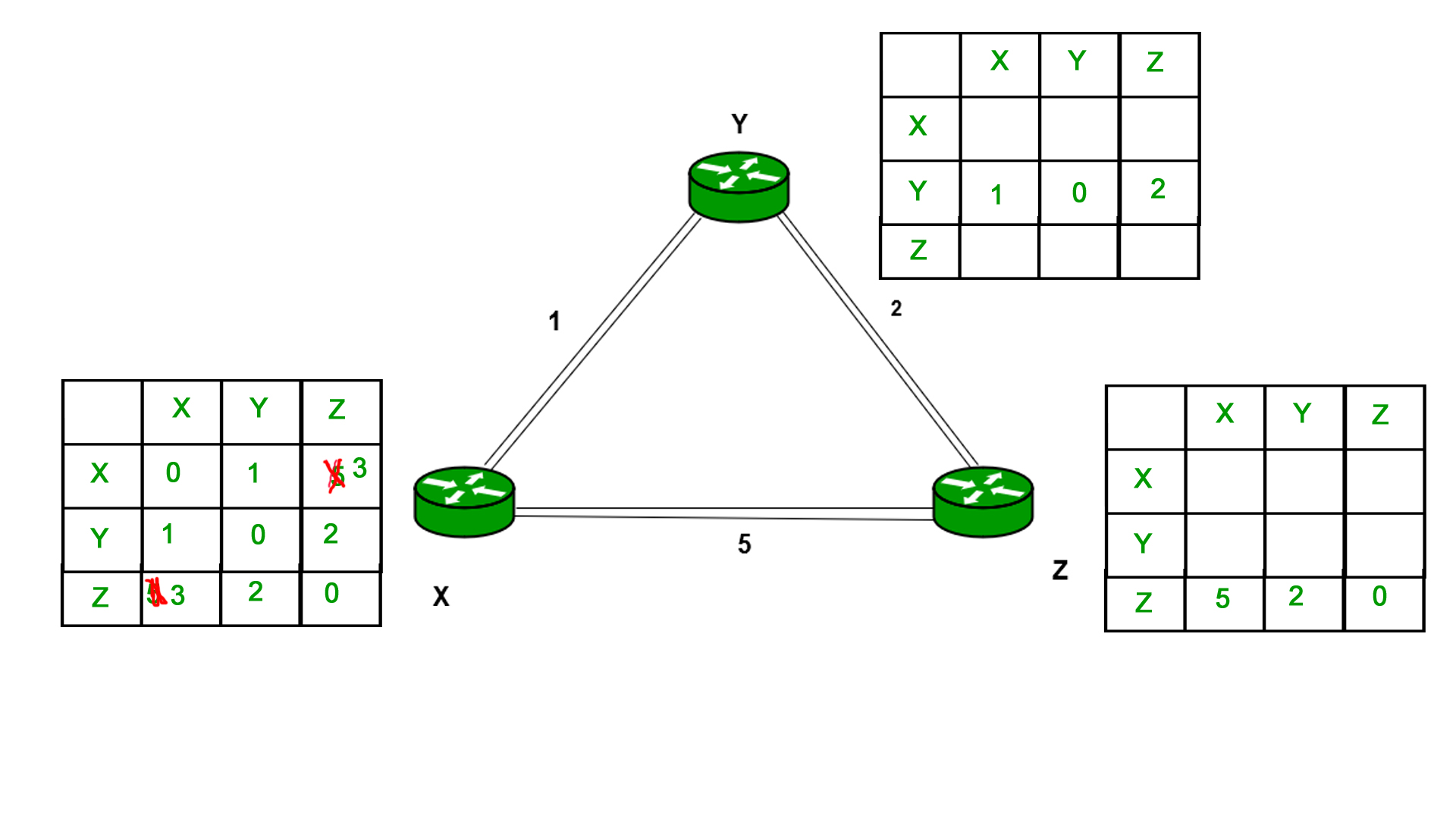
类似地,对于Z也–
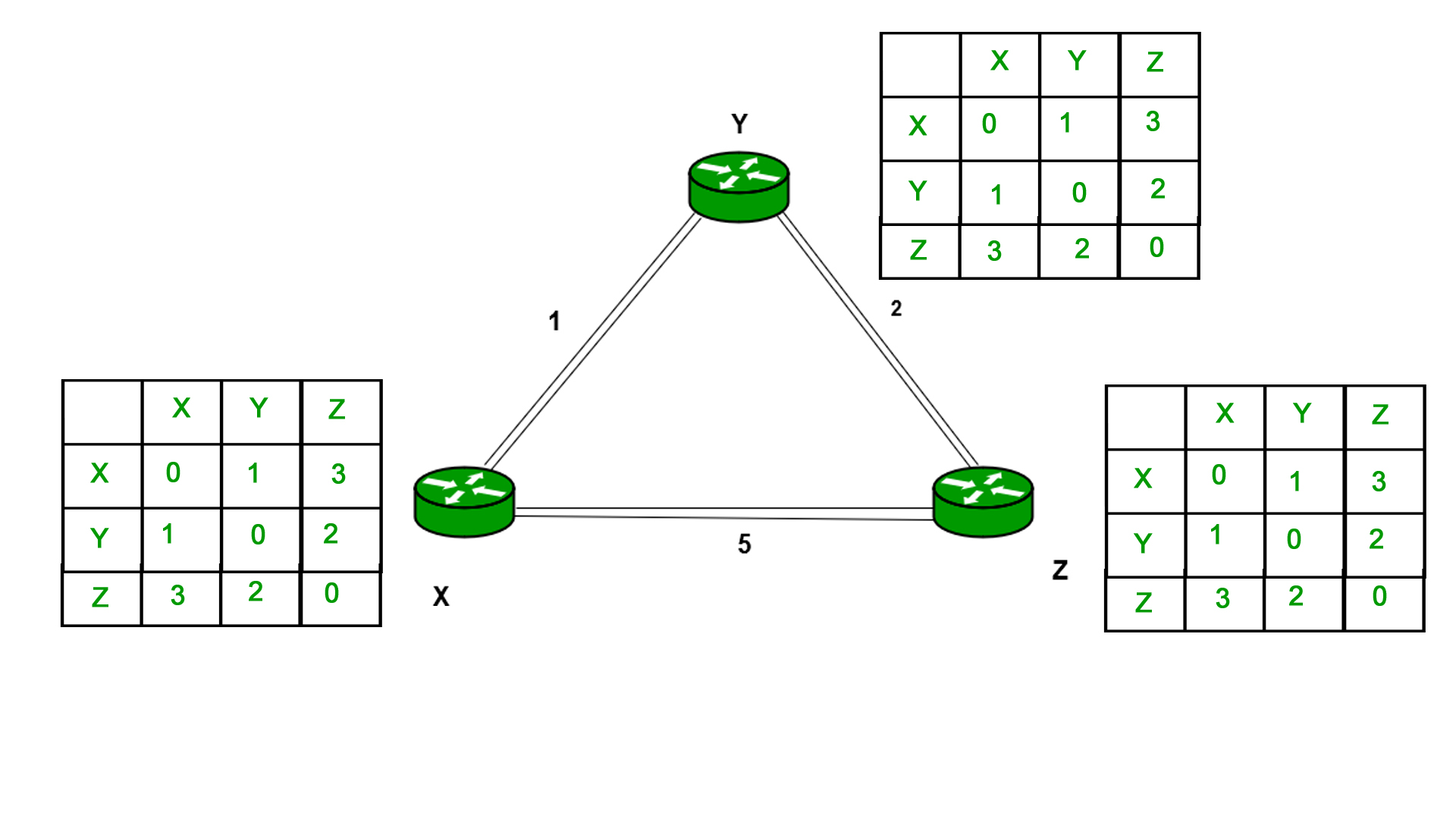
最后是所有人的路由表–
距离矢量路由的优点–
- 它比链接状态路由更易于配置和维护。
- 收敛比链接状态慢。
- 它受到计数到无穷大问题的威胁。
- 由于跳数更改必须传播到所有路由器并在每个路由器上进行处理,因此它产生的流量超过链接状态。即使网络拓扑没有变化,跳数更新也会定期进行,因此仍然会浪费带宽。
- 对于较大的网络,距离矢量路由生成的路由表比链路状态大,因为每个路由器都必须知道所有其他路由器。这也可能导致WAN链路拥塞。
