给定一个图和图中的一个源顶点,找到从源到给定图中所有顶点的最短路径。
Dijkstra的算法与最小生成树的Prim算法非常相似。像Prim的MST一样,我们以给定的源为根来生成SPT(最短路径树)。我们维护两组,一组包含最短路径树中包含的顶点,另一组包含尚未包含在最短路径树中的顶点。在算法的每个步骤中,我们都找到一个顶点,该顶点在另一个集合中(尚未包含),并且与源的距离最小。
以下是Dijkstra算法中用于查找从单个源顶点到给定图中所有其他顶点的最短路径的详细步骤。
算法
1)创建一个set sptSet(最短路径树集合),该集合跟踪最短路径树中包含的顶点,即,其与源的最小距离已被计算并确定。最初,此集合为空。
2)为输入图中的所有顶点分配一个距离值。将所有距离值初始化为INFINITE。将源顶点的距离值指定为0,以便首先拾取它。
3)虽然sptSet不包括所有顶点
…。a)选择一个在sptSet中不存在的顶点u并具有最小距离值。
…。b)将u包含到sptSet中。
…。c)更新u的所有相邻顶点的距离值。要更新距离值,请遍历所有相邻的顶点。对于每个相邻顶点v,如果u(来自源)的距离值和边缘uv的权重之和小于v的距离值,则更新v的距离值。
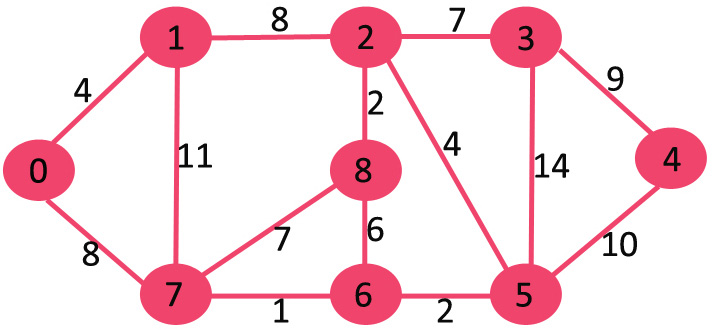
让我们用下面的例子来理解:
集合sptSet最初为空,并且分配给顶点的距离为{0,INF,INF,INF,INF,INF,INF,INF},其中INF表示无穷大。现在选择距离最小的顶点。选择顶点0,将其包含在sptSet中。因此,sptSet变为{0}。将0包含到sptSet之后,更新其相邻顶点的距离值。0的相邻顶点为1和7。1和7的距离值更新为4和8。下图显示了顶点及其距离值,仅显示了具有有限距离值的顶点。SPT中包含的顶点显示为绿色。
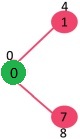
选择具有最小距离值且尚未包含在SPT中的顶点(不在sptSET中)。选择顶点1并将其添加到sptSet。因此,sptSet现在变为{0,1}。更新相邻顶点的距离值1。顶点2的距离值变为12。
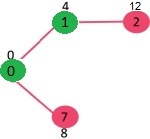
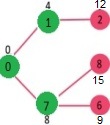
选择具有最小距离值且尚未包含在SPT中的顶点(不在sptSET中)。选择了顶点7。因此,sptSet现在变为{0,1,7}。更新相邻顶点7的距离值。顶点6和8的距离值变得有限(分别为15和9)。
选择具有最小距离值且尚未包含在SPT中的顶点(不在sptSET中)。选择了顶点6。因此,sptSet现在变为{0,1,7,6}。更新相邻顶点6的距离值。更新顶点5和8的距离值。
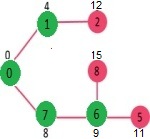
我们重复上述步骤,直到sptSet确实包含给定图的所有顶点为止。最后,我们得到以下最短路径树(SPT)。
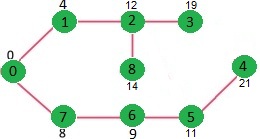
如何实现以上算法?
C ++
// A C++ program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph
#include <limits.h>
#include <stdio.h>
// Number of vertices in the graph
#define V 9
// A utility function to find the vertex with minimum distance value, from
// the set of vertices not yet included in shortest path tree
int minDistance(int dist[], bool sptSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min)
min = dist[v], min_index = v;
return min_index;
}
// A utility function to print the constructed distance array
void printSolution(int dist[])
{
printf("Vertex \t\t Distance from Source\n");
for (int i = 0; i < V; i++)
printf("%d \t\t %d\n", i, dist[i]);
}
// Function that implements Dijkstra's single source shortest path algorithm
// for a graph represented using adjacency matrix representation
void dijkstra(int graph[V][V], int src)
{
int dist[V]; // The output array. dist[i] will hold the shortest
// distance from src to i
bool sptSet[V]; // sptSet[i] will be true if vertex i is included in shortest
// path tree or shortest distance from src to i is finalized
// Initialize all distances as INFINITE and stpSet[] as false
for (int i = 0; i < V; i++)
dist[i] = INT_MAX, sptSet[i] = false;
// Distance of source vertex from itself is always 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum distance vertex from the set of vertices not
// yet processed. u is always equal to src in the first iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent vertices of the picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in sptSet, there is an edge from
// u to v, and total weight of path from src to v through u is
// smaller than current value of dist[v]
if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX
&& dist[u] + graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
// print the constructed distance array
printSolution(dist);
}
// driver program to test above function
int main()
{
/* Let us create the example graph discussed above */
int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(graph, 0);
return 0;
} Java
// A Java program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph
import java.util.*;
import java.lang.*;
import java.io.*;
class ShortestPath {
// A utility function to find the vertex with minimum distance value,
// from the set of vertices not yet included in shortest path tree
static final int V = 9;
int minDistance(int dist[], Boolean sptSet[])
{
// Initialize min value
int min = Integer.MAX_VALUE, min_index = -1;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min) {
min = dist[v];
min_index = v;
}
return min_index;
}
// A utility function to print the constructed distance array
void printSolution(int dist[])
{
System.out.println("Vertex \t\t Distance from Source");
for (int i = 0; i < V; i++)
System.out.println(i + " \t\t " + dist[i]);
}
// Function that implements Dijkstra's single source shortest path
// algorithm for a graph represented using adjacency matrix
// representation
void dijkstra(int graph[][], int src)
{
int dist[] = new int[V]; // The output array. dist[i] will hold
// the shortest distance from src to i
// sptSet[i] will true if vertex i is included in shortest
// path tree or shortest distance from src to i is finalized
Boolean sptSet[] = new Boolean[V];
// Initialize all distances as INFINITE and stpSet[] as false
for (int i = 0; i < V; i++) {
dist[i] = Integer.MAX_VALUE;
sptSet[i] = false;
}
// Distance of source vertex from itself is always 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum distance vertex from the set of vertices
// not yet processed. u is always equal to src in first
// iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent vertices of the
// picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in sptSet, there is an
// edge from u to v, and total weight of path from src to
// v through u is smaller than current value of dist[v]
if (!sptSet[v] && graph[u][v] != 0 && dist[u] != Integer.MAX_VALUE && dist[u] + graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
// print the constructed distance array
printSolution(dist);
}
// Driver method
public static void main(String[] args)
{
/* Let us create the example graph discussed above */
int graph[][] = new int[][] { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
ShortestPath t = new ShortestPath();
t.dijkstra(graph, 0);
}
}
// This code is contributed by Aakash Hasija Python
# Python program for Dijkstra's single
# source shortest path algorithm. The program is
# for adjacency matrix representation of the graph
# Library for INT_MAX
import sys
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
def printSolution(self, dist):
print "Vertex \tDistance from Source"
for node in range(self.V):
print node, "\t", dist[node]
# A utility function to find the vertex with
# minimum distance value, from the set of vertices
# not yet included in shortest path tree
def minDistance(self, dist, sptSet):
# Initilaize minimum distance for next node
min = sys.maxint
# Search not nearest vertex not in the
# shortest path tree
for v in range(self.V):
if dist[v] < min and sptSet[v] == False:
min = dist[v]
min_index = v
return min_index
# Funtion that implements Dijkstra's single source
# shortest path algorithm for a graph represented
# using adjacency matrix representation
def dijkstra(self, src):
dist = [sys.maxint] * self.V
dist[src] = 0
sptSet = [False] * self.V
for cout in range(self.V):
# Pick the minimum distance vertex from
# the set of vertices not yet processed.
# u is always equal to src in first iteration
u = self.minDistance(dist, sptSet)
# Put the minimum distance vertex in the
# shotest path tree
sptSet[u] = True
# Update dist value of the adjacent vertices
# of the picked vertex only if the current
# distance is greater than new distance and
# the vertex in not in the shotest path tree
for v in range(self.V):
if self.graph[u][v] > 0 and sptSet[v] == False and \
dist[v] > dist[u] + self.graph[u][v]:
dist[v] = dist[u] + self.graph[u][v]
self.printSolution(dist)
# Driver program
g = Graph(9)
g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]
];
g.dijkstra(0);
# This code is contributed by Divyanshu Mehta 输出:
顶点到源的距离 0 0 1 4 2 12 3 19 4 21 5 11 6 9 7 8 8 14
注意:
1)该代码计算最短距离,但不计算路径信息。我们可以创建一个父数组,在更新距离时更新父数组(例如prim的实现),并使用它显示从源到不同顶点的最短路径。
2)该代码用于无向图,相同的dijkstra函数也可用于有向图。
3)代码查找从源到所有顶点的最短距离。如果我们在最短的距离只关心从源到单个目标,我们可以在拾取最小距离顶点等于目标(该算法的步骤3.A)打破的循环。
4)实现的时间复杂度为O(V ^ 2)。如果使用邻接表表示输入图,则可以在二进制堆的帮助下将其简化为O(E log V)。有关更多详细信息,请参见
Dijkstra的邻接列表表示算法。
5) Dijkstra的算法不适用于负周期为负的图,它可能为具有负边的图给出正确的结果。对于负边沿和周线为负的图形,可以使用Bellman-Ford算法,我们很快将在单独的文章中进行讨论。
