虽然我相信我们都同意队列是自切片面包以来最酷的东西,但我们实际上可以通过将它们与称为堆的树的变体混合来做得更好。使用堆,我们可以将我们的数据构建到一个更智能的队列中,该队列按重要性而不是顺序排序。
概念
与二叉搜索树不同,我们在兄弟姐妹之间比较和组织我们的值,而堆我们只在父母和他们的孩子之间工作。这为我们提供了两种堆的可能性,themax heap和 the min heap,无论您是从最高值移动到最低值,反之亦然。为简单起见,我们只关注最大堆,因为将其转换为最小堆非常容易。
与二叉搜索树一样,二叉堆只允许一个父节点有两个或更少的子节点。它们也很特别,因为它们总是平衡的,因为每个新节点都会从左到右添加到一个级别,直到满为止。
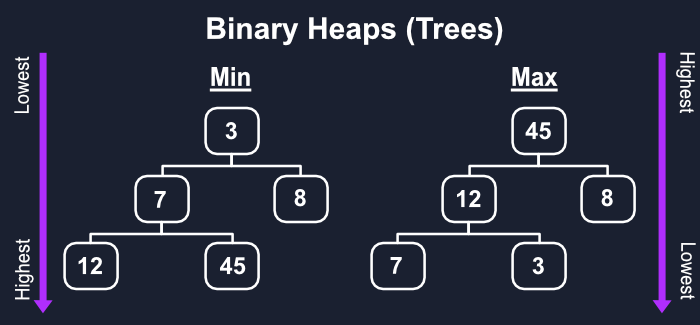
遗憾的是,链表通常不是二叉堆的最佳方法,尽管它通常被概念化为具有左右孩子的树,尽管它仍然是可能的。
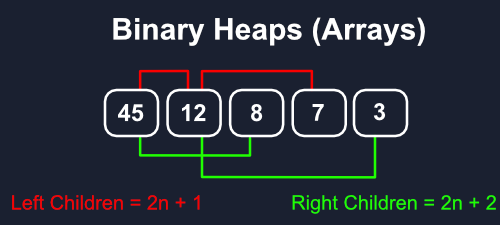
大多数情况下,将其作为数组处理会更好,所以这就是我们将在这里介绍的内容。顺序与您所期望的一样,在移动到下一个级别之前,所有内容都在一个级别上从左到右。
这样,我们创建了一个非常一致的模式来查找节点的子节点。节点的所有左子节点都将正好位于2n + 1远离其父节点的位置,n作为其父节点的索引,所有右子节点都为2n + 2。
添加节点
看起来添加一个新节点就像推入我们的数组一样简单,但棘手的部分是我们需要将它与自身和最大值之间的父节点进行比较,然后相应地对它们重新排序。

图形/动画感谢VisuAlgo.net
在我们将我们的新项目推到数组的末尾之后,我们需要“冒泡”我们更大的值。首先,我们需要获取数组末尾的新项,我们将分解为索引和该索引处的新项。
每次我们添加一个项目时,我们将使用我们的等式的逆来查找子项,(n-1)/2,以找到其父项。如果它的父节点小于当前节点,交换它们然后保存它的索引,这将是下一个current. 这将一直持续到没有父母离开。
由于它将逐渐index从末尾向上移动,只要它大于零,就继续交换。
class BH {
constructor() {
this.values = [];
}
add(element) {
this.values.push(element);
let index = this.values.length - 1;
const current = this.values[index];
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2);
let parent = this.values[parentIndex];
if (parent <= current) {
this.values[parentIndex] = current;
this.values[index] = parent;
index = parentIndex;
} else break;
}
}
}
const tree = new BH();
tree.add(3);
tree.add(4);
tree.add(31);
tree.add(6);
console.log(tree); // [31, 6, 4, 3]
删除最大值
删除最顶层的节点比您想象的要复杂一些。我们将返回第一个节点,即我们的最大值,然后取最后一个节点,即数组的末尾,并将其设置为新的最大值。
我们这样做是为了我们可以使用我们的最低值作为一个简单的基线来与我们的其他值进行比较,因为我们在进行比较和交换的同时“下沉”回到树的底部。
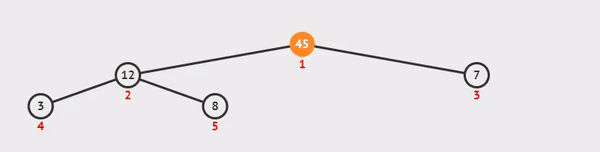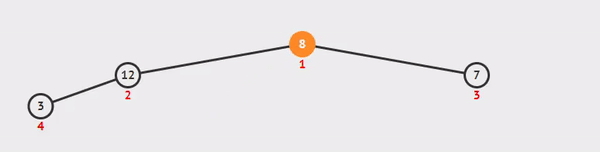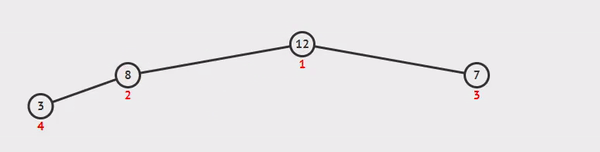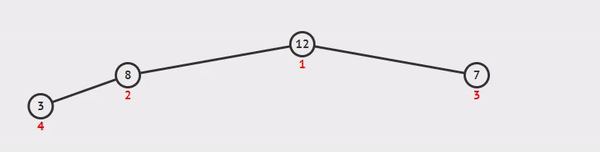
图形/动画感谢VisuAlgo.net
简单的部分是获取我们当前的最大值并在将其替换为最后一项之前将其弹出,然后我们可以在其他一切完成后返回我们的原始最大值。
一旦我们有了一个起始索引,我们就想同时获取它的左右孩子。如果左孩子是一个有效的项目并且更大,那么我们可以将其保存为swap在所有比较完成后运行交换。
右孩子有点复杂,我们只想要一个最大的孩子与父母交换。我们将添加一个单独的要求,rightChild只能将其设置为swap尚未定义或大于leftChild.
class BH {
extractMax() {
const max = this.values[0];
const end = this.values.pop();
this.values[0] = end;
let index = 0;
const length = this.values.length;
const current = this.values[0];
while (true) {
let leftChildIndex = 2 * index + 1;
let rightChildIndex = 2 * index + 2;
let leftChild, rightChild;
let swap = null;
if (leftChildIndex < length) {
leftChild = this.values[leftChildIndex];
if (leftChild > current) swap = leftChildIndex;
}
if (rightChildIndex < length) {
rightChild = this.values[rightChildIndex];
if (
(swap === null && rightChild > current) ||
(swap !== null && rightChild > leftChild)
)
swap = rightChildIndex;
}
if (swap === null) break;
this.values[index] = this.values[swap];
this.values[swap] = current;
index = swap;
}
return max;
}
}
const tree = new BH();
tree.add(3);
tree.add(4);
tree.add(31);
tree.add(6);
console.log(tree.extractMax()); // 31
优先队列
通过一些小的调整,我们可以将二进制堆与队列混合,并创建一种队列类型,按重要性而不是添加时间来组织我们的数据。
我们可以通过存储节点而不是单个数字来简单地实现这一点。每个节点都有一个优先级(比方说从 1 到 5),它将用于确定顺序。当两个节点上的优先级相同时,左子节点因为先添加,所以会先添加。
我们所要做的就是priority每次在if语句中进行比较时使用节点的。
class Node {
constructor(val, priority) {
this.val = val;
this.priority = priority;
}
}
class PQ {
constructor() {
this.values = [];
}
enqueue(val, priority) {
let newNode = new Node(val, priority);
this.values.push(newNode);
let index = this.values.length - 1;
const current = this.values[index];
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2);
let parent = this.values[parentIndex];
if (parent.priority <= current.priority) {
this.values[parentIndex] = current;
this.values[index] = parent;
index = parentIndex;
} else break;
}
}
dequeue() {
const max = this.values[0];
const end = this.values.pop();
this.values[0] = end;
let index = 0;
const length = this.values.length;
const current = this.values[0];
while (true) {
let leftChildIndex = 2 * index + 1;
let rightChildIndex = 2 * index + 2;
let leftChild, rightChild;
let swap = null;
if (leftChildIndex < length) {
leftChild = this.values[leftChildIndex];
if (leftChild.priority > current.priority) swap = leftChildIndex;
}
if (rightChildIndex < length) {
rightChild = this.values[rightChildIndex];
if (
(swap === null && rightChild.priority > current.priority) ||
(swap !== null && rightChild.priority > leftChild.priority)
)
swap = rightChildIndex;
}
if (swap === null) break;
this.values[index] = this.values[swap];
this.values[swap] = current;
index = swap;
}
return max;
}
}
const tree = new BH();
tree.enqueue(3, 2);
tree.enqueue(4, 5);
tree.enqueue(31, 1);
tree.enqueue(6, 3);
console.log(tree.dequeue()); // 4
console.log(tree.dequeue()); // 6
console.log(tree.dequeue()); // 3
console.log(tree.dequeue()); // 31
闭幕式
就像我们如何使用标准队列进行树遍历一样,优先队列对于智能遍历图和更复杂的结构至关重要。
将最大堆转换为最小堆就像在所有比较中将大于号更改为小于号一样简单。
